问题
问答题
设函数
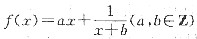，曲线y=f(x)在点(2，f(2))处的切线方程为y=3．
求f(x)的解析式，并证明：函数y=f(x)的图像是一个中心对称图形，并求其对称中心；
答案
参考答案：
[解] [*]，因为(2，f(2))在直线y=3上，故f(2)=3，
于是[*]解得[*]或[*]
因a，b∈Z，故[*]
证明：已知函数y1=x，[*]都是奇函数．
所以函数[*]也是奇函数，其图像是以原点为中心的中心对称图形．
而[*]
可知，函数g(x)的图像按向量a=(1，1)平移，即得到函数f(x)的图像，故函数f(x)的图像是以点(1，1)为中心的中心对称图形．