如图所示，水平面上放有质量均为m=1kg的物块A和B（均视为质点）

问题填空题

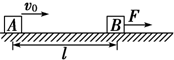
如图所示，水平面上放有质量均为m=1kg的物块A和B（均视为质点），A、B与地面的动摩擦因数分别为μ₁=0.4和μ₂=0.1，相距L=0.75m．现给物块A一初速度v₀使之向物块B运动，与此同时给物块B一个F=3N水平向右的力使其由静止开始运动，取g=10m/s²．求：

（1）物块B运动的加速度大小；

（2）若要使A能追上B，v₀应满足什么条件？

答案

（1）对B，由牛顿第二定律得：F-μ₂mg=ma_B

解得a_B=2 m/s²．

即物块B运动的加速度大小为2 m/s²．

（2）设物块A经过t时间追上物块B，对物块A，由牛顿第二定律得：

μ₁mg=ma_A

x_A=v₀t-

a_At²

x_B=

a_Bt²

恰好追上的条件为：v₀-a_At=a_Bt

x_A-x_B=l

联立各式并代入数据解得：t=0.5 s，v₀=3 m/s．

即若要使A能追上B，v₀应不小于3m/s．