问题
填空题
等腰三角形的顶角是120°，底边上的中线长为4cm,则它的腰长是 ；
答案
8cm
如图，AB=AC，AD是底边BC的中线，
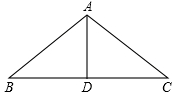∴AD⊥BC，AD=4cm，∠BAC=120°，
∵∠BAC=120°，AB=AC
∴∠B=∠C=（180°-∠BAC）÷2=30°
∴AB=2AD=8cm（30°角所对的直角边是斜边的一半）．
故答案为：8．
搜题请搜索小程序“爱下问搜题”
等腰三角形的顶角是120°，底边上的中线长为4cm,则它的腰长是 ；
8cm
如图，AB=AC，AD是底边BC的中线，
∴AD⊥BC，AD=4cm，∠BAC=120°，
∵∠BAC=120°，AB=AC
∴∠B=∠C=（180°-∠BAC）÷2=30°
∴AB=2AD=8cm（30°角所对的直角边是斜边的一半）．
故答案为：8．