问题
问答题
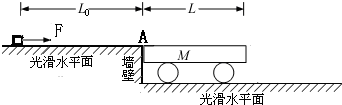
如图所示,有两个高低不同的光滑水平面,一质量M=5kg、长L=2m的平板车靠高水平面边缘A点放置,上表面恰好与高水平面平齐.一质量m=1kg可视为质点的滑块静止放置,距A点距离为L0=3m,现用大小为6N、水平方向的外力F拉小滑块,当小滑块运动到A点时撤去外力,滑块以此时的速度滑上平板车.滑块与平板车间的动摩擦因数μ=0.5,取
g=10m/s2.
(1)求滑块滑动到A点时的速度大小;
(2)求滑块滑动到平板车上时,滑块和平板车的加速度大小分别为多少?
(3)通过计算说明滑块能否从平板车的右端滑出.
答案
(1)根据动能定律有:FL0=
m1 2
-0v 20
解得:v0=6m/s.
故滑块滑动到A点时的速度大小为:v0=6m/s.
(2)根据牛顿第二定律有:
对滑块有:mgμ=ma1,解得滑块的加速度大小为:a1=5m/s2;
对平板车有:mgμ=Ma2,解得平板车加速度大小为:a2=1m/s2.
故滑块滑动到平板车上时,滑块和平板车的加速度大小分别为a1=5m/s2,a2=1m/s2.
(4)设平板车足够长,小滑块与平板车速度相等时:v0-a1t=a2t
得:t=1s,则此时小滑块位移:x1=v0t-
at2=3.5m1 2
平板车位移:x2=
a2t2=0.5m1 2
x1-x2>L
所以小滑块滑出平板车右端.
