问题
填空题
曲线y=x3+3x2-5上与直线2x-6y+3=0垂直的切线方程为______．
答案
参考答案：3x+y+6=0
解析：[详解] 设切点为(x0，y0)，则切线斜率为：
．
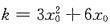又因为直线2x-6y+3=0的斜率为：
，
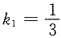所以
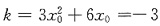，解之得x0=-1，y0=-3．
故所求切线方程为：y+3=-3(x+1)，即3x+y+6=0．
搜题请搜索小程序“爱下问搜题”
曲线y=x3+3x2-5上与直线2x-6y+3=0垂直的切线方程为______．
参考答案：3x+y+6=0
解析：[详解] 设切点为(x0，y0)，则切线斜率为：
．
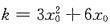又因为直线2x-6y+3=0的斜率为：
，
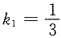所以
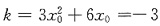，解之得x0=-1，y0=-3．
故所求切线方程为：y+3=-3(x+1)，即3x+y+6=0．