问题
单项选择题
设函数f(x)在[-1，1]上有定义，在x=0处可导，则f’(0)=0是级数
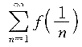收敛的
A．充分条件．
B．必要条件．
C．充分必要条件．
D．既非充分也非必要条件．
答案
参考答案：B
解析：[详解] 如果级数
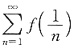收敛，则
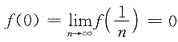，且有
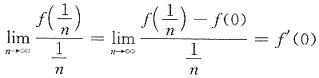
如果f’(0)≠0，不妨设f’(0)＞0，则由极限保号性，当n充分大时，
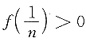，且当n→∞时，
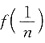与
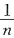是同阶无穷小，所以由比较判别法，级数
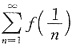发散，出现矛盾．
同理，当f’(0)＜0时，级数
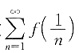也发散．
故f’(0)=0是级数
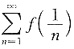收敛的必要条件．
如果f’(0)=0，不一定能得到f(0)=0及
，所以不能得到级数
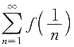收敛．
因此，f’(0)=0是级数
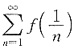收敛的必要而非充分条件，故选(B)．