问题
问答题
设曲线L位于xOy平面的第一象限内，L上任意一点M处的切线与y轴总相交，交点为A，已知|MA|=|OA|，且L经过点（1，1），求L的方程。
答案
参考答案：
设点M的坐标为(x，y)，则切线MA：Y-y=y’(X=x)，令X=0，则Y=y-y’x，故点A的坐标为(0，y-y’x)．
由 |MA|=|OA|，得
即
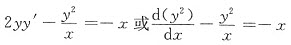这是一阶线性非齐次方程，得解，
因为曲线经过点(1，1)，所以C=2．
再由曲线在第一象限内，得曲线方程为
。