问题
问答题
设函数z=f(x，y)在点(1，1)处可微，且f(1，1)=1，
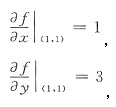
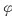(x)=f(x，xf(x，x))，求。
答案
参考答案：
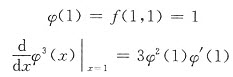，归结为求
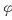’(1)．
根据复合函数求导法得
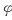’(x)=f’1(x，xf(x，x))+f’2(x，xf(x，x))·
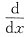[xf(x，x)]
=f’1(x，xf(x，x))+f’2(x，xf(x，x))·
{f(x，x)+x[f’1(x，x)+f’2(x，x)]}
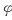’(1)=f’1(1，1)+f’2(1，1)[1+f’1(1，1)+f’2(1，1)]此处
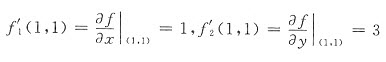所以
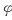’(1)=1+3×(1+1+3)=16
．
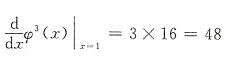