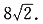问题
问答题
如图，已知直线L：y=kx-2与抛物线C：x2=-2py(p＞0)交于A、B两点，O为坐标原点，
，求：
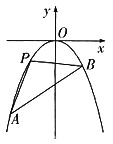
（1）求直线L和抛物线C的方程；
（2）抛物线上一动点P从A到B运动时，求△ABP面积的最大值．
答案
参考答案：
(1)因为：
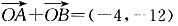，即xA+xB=-4，yA+yB=-12
可以得到AB中点坐标是(-9，-6)
又因为L：y=kx-2
所以代入算得：y=2x-2
代入C：x2=-2py(p＞0)
得到：x2+4px-4p=0
根据韦伯公式：x1+x2=-4p
又因为x1-x2=-4
所以p=1
所以C：x2=-2y
(2)设点P为
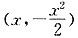
然后用点到直线的距离公式算出
又因为
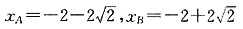
因此：d的最大值是当x=-2时，
再因为
所以面积最大值是