问题
问答题
把函数
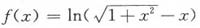展开成x的幂级数，并指出这个幂级数展开式成立的范围．
答案
参考答案：将f(x)求导即得
[*]
利用(1+x)α的幂级数展开式
[*]
令[*]，并把x换为x2即得f’(x)的幂级数展开式
[*]
其中(2n-1)!!=1·3·5…(2n-1)，(2n)!!=2·4·6…(2n)．利用f(0)=0，在(-1，1)上逐项积分即得f(x)的幂级数展开式
[*]
以上幂级数在点x=1处成为交错级数
[*]
由于数列[*]单调减少且趋于零，故幂级数在点x=1处收敛，类似可知幂级数在点x=-1处也收敛，又因函数[*]在x=-1与x=1处都连续，故f(x)的幂级数展开式不仅在(-1，1)内成立，而且在点x=-1与x=1也成立，即
[*]