问题
问答题
计算累次积分
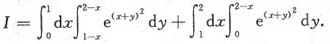
答案
参考答案:在本题中无法写出函数[*]的原函数,所以直接计算行不通,可行的方法之一是把直角坐标转换为极坐标,方法之二是在内层积分中作换元t=x+y.
[解法一] 由题设知累次积分I可以写成积分区域D=D1+D2上的二重积分[*],其中D1={(x,y)|0≤x≤1,1-x≤y≤2-x},D2={(x,y)|1≤x≤2,0≤y≤2-x},如右图所示.令x=rcosθ,y=rsinθ,在极坐标系(r,θ)中[*],从而
[*]
[*]
[解法二] 在内层积分作换元t=x+y,于是y:1-x→2-x[*]t:1→2,y:0→2-X[*]t:x→2,且dt=dy,从而
[*]
[*]
其中D0=D01+D02,且D01={(x,t)|0≤x≤1,1≤t≤2},D02={(x,t)|1≤x≤2,x≤t≤2},如右图所示.注意积分区域D0又可表示为D0={(x,t)|1≤t≤2,0≤x≤t
