问题
单项选择题
若f(x，y)在区域。内具有二阶偏导数：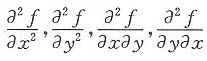
，则（）。
A．必有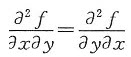
B．f(x,y)在D内必连续
C．f(x，y)在D内必可微
D．三个结论都不对
答案
参考答案：A
解析：
偏导数存在与函数f(x，y)的连续性及可微性的关系，与一元函数的情况大不相同，主要表现在偏导数的存在与函数的连续性没有必然的联系．
考虑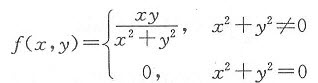
可以验证选项(A)、(B)、(C)均不成立，仅(D)入选．
事实上，f(x，y)在点(0，0)处不连续．因当y=kx时，有
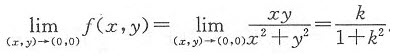
当k取不同值时，
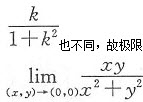不存在，因而在点(0，0)处f(x，y)不连续．又因f(x，y)在点(0，0)处可微的必要条件是f(x，y)在点(0，0)处连续，故f(x，y)在点(0，0)处也不可微．(C)也不成立．
二阶偏导数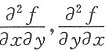
存在且连续时，才有
。
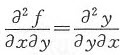它们是否连续，题中未作交待．故(A)也不成立．