设向量α1,α2,…,αr是齐次线性方程组Ax=0的一个基础解系,向量β不是方程组Ax=0的解.
证明:向量组β,β+α1,β+α2,…,β+αr线性无关。
参考答案:
对于抽象向量组的线性相关性的证明常用定义证之.注意到待证线性无关的向量组可以看成是一组可以写成另一组向量β,α1,α2,…,αn的线性组合的向量组.如能证明β1,α1,α2,…,αn线性无关,则可用矩阵表示法证之.
证一 设有一组数k,k1,k2,…,kr,使

由于α1,α2,…,αr为Ax=0的基础解系,α1,α2,αr必线性无关,故
k1=k2=…=kr=0.
③
将式③代入式②得k=0,故向量组β,β+α1,β+α2,…,β+αr线性无关.
证二 用矩阵表示法证之.
先证α1,α2,…,αn,β线性无关,可用反证法证之.如果α1,α2,…,αn,β线性相关,而α1,α2,…,αn线性无关,故β可由α1,α2,…,αn线性表示.设
β=k1α1+k2α2+…+knαn.
在上式两端左乘A,得到
Aβ=k1Aα1+k2Aα2+…+knAαn=0+0+…+0=0.
这与Aβ≠0矛盾,故α1,α2,…,αn,β线性无关.又因
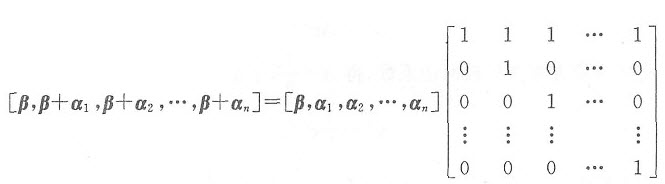
=[β,α1,α2,…,αn]K.
显然|K|=1≠0,故β,β+α1,β+α2,…,β+αn线性无关.
