参考答案：

先求区域内的极值，再求边界上的极值，通过比较即得闭区域上的最值．

由方程组

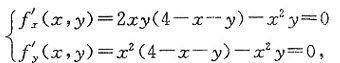
得x=0(0≤y≤6)及点(4，0)，(2，1)．

点(4，0)及线段x=0在D的边界上，且f(2，1)=4．

在边界x+y=6上，y=6-x，代入f(x，y)中，得

z=2x³-12x² (0≤x≤6)．

由z’=6x²-24x=0得x=0，x=4．

当x=0时，y=6，f(0，6)=0．

当x=4时，y=2，f(4，2)=-64．

经比较，最大值为f(2，1)=4，最小值为f(4，2)=-64．

注意求连续函数z=f(x，y)在有界闭区域D上最值的步骤如下：

(1)求D内的驻点(即方程组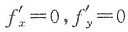的解)及不可导点(即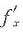与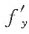不存在的点)；

(2)将D的边界线方程代入z=f(x，y)中将其化为一元函数，求出其极值可疑点(即z’=0的根及使z’不存在的点)；

(3)求出上述所有点处对应的函数值，比较其大小，可得f(x，y)在D上的最大值与最小值．