某公司在2002年1月1日发行一种债券,每张面值为1000元,其票面利率为10%,期限为5年。回答下列各不相关的问题。(计算过程中保留小数点后4位,计算结果保留小数点后2位。)
[要求]
(1)如果该债券每年计算并支付两次利息,到期偿还本金,若发行时按1050元溢价购入,要求计算该债券的到期收益率;
(2)如果该债券为每年12月31日付息,2005年1月1日购入时的市场利率下降到8.24%。那么此时债券的价值是多少
(3)如果该债券为单利计息,到期一次还本付息,2005年1月1日的市价为1300元,此时购买该债券的到期收益率是多少
(4)如果该债券的β值为0.8,证券市场平均收益率为9%,现行国库券的收益率为6%,计算该债券的预期收益率。
(5)如果在2005年12月1日购入该债券,投资的必要报酬率为10%,投资人愿意支付的最高价格是多少
参考答案:
(1)每期利息=1000×(10%÷2)=50(元);期数=5×2=10(期)
债券购人价格=未来现金流入现值
1050=50×(P/A,i,10)+1000×(P/S,i,10)由于溢价购入,市场利率低于票面利率,用i= 4%试算:
50×(P/A,4%,10)+1000×(P/S,4%,10)
=50×8.1109+1000×0.6756
=405.55+675.60
=1081.15(元)
由于贴现结果大于1050元,应提高贴现率再试算。
用i=5%试算:
50×(P/A,5%,10)+1000×(P/S,5%,10)
=50×7.7217+1000×0.6139
=386.09+613.90=1000(元)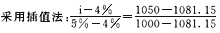
求得:i=4.38%
该债券的到期收益率=4.38%×2=8.76%
(2)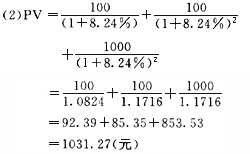
=92.39+85.35+853.53
=1031.27(元)
此时该债券的价值为1031.27(元)
(3)债券到期本利和
=1000×(1+10%×5)=1500(元)
1300=1500×(P/S,i,2)
(P/S,i,2)=1300/1500=0.8667
查表:(P/S,7%,2)=0.8734;(P/S,8%,2)
=0.8573
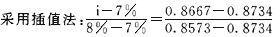
i=7.42%
此时该债券的到期收益率为7.42%
(4)采用资本资产定价模式计算:
该债券预期收益率
=6%+0×8×(9%-6%)
=6%-2.4%=8.4%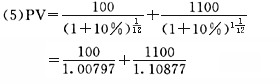
=99.21+992.09=1091.30(元)
