问题
填空题
设函数z=f(x，y)(xy≠0)满足
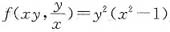，则dz=______．
答案
参考答案：(2x-y)dx-xdy．
解析：
[分析]： 设xy=u，[*]，有[*]，y2=uv．
[*]
即 f(x，y)=x2-xy．
所以 dz=(2x-y)dx-xdy．
搜题请搜索小程序“爱下问搜题”
设函数z=f(x，y)(xy≠0)满足
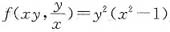，则dz=______．
参考答案：(2x-y)dx-xdy．
解析：
[分析]： 设xy=u，[*]，有[*]，y2=uv．
[*]
即 f(x，y)=x2-xy．
所以 dz=(2x-y)dx-xdy．