如图所示，倾角θ=37°的斜面上有一个质量m=3.5kg的小物体．用大小F=5N

问题问答题

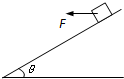
如图所示，倾角θ=37°的斜面上有一个质量m=3.5kg的小物体．用大小F=5N的水平拉力从静止起拉动物体，t=

s后，经过位移S=5m到达斜面底端．（sin37°=0.6，cos37°=0.8）

（1）物体的加速度a

（2）物体与斜面的动摩擦因数μ

（3）改变水平外力F的大小，使小物体以最短时间沿斜面到达斜面底端，求最短时间．

答案

（1）根据匀加速直线运动位移时间公式得：

at^{2
解得：a=
2s
t2
=10
7
=1.43m/s²
（2）以物体为研究对象，根据牛顿第二定律有
Fcosθ+mgsinθ-f=ma
而f=μN
N=mgcosθ-Fsinθ
整理得：
4+21-μ（28-3）=5
解得：μ=0.8
（3）根据（2）中列式可知，外力增大引起加速度增大，外力增大引起弹力减小，为了保证物块不脱离斜面，外力最大值出现在弹力为零时．
以物体为研究对象有
mg
sinθ
=ma
a=
g
sinθ
=16.7m/s²
根据s=
1
2
at²
解得：t=
0.6
s=0.77s
答：（1）物体的加速度为1.43m/s²；
（2）物体与斜面的动摩擦因数μ为0.8；
（3）最短时间为0.77s．}