问题
单项选择题
下列矩阵
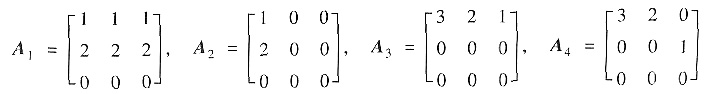
中两两相似的是
A．A3，A4.
B．A1，A2.
C．A1，A3.
D．A2，A3.
答案
参考答案：C
解析：判断相似应当用相似的必要条件作第一轮判别，相似的必要条件是：特征值一样，秩相等，…
A3，A4虽特征值一样，但秩不相等，所以不相似. A1与A2或A2与A3虽秩相等但特征值不一样，因此不相似. 用排除法知应选C.
实际上，A1，A3的特征值都是3，0，0，且r(0E-A1)=1，r(0E-A3)=1，则
n-r(0E-A1)=3-1=2，n-r(0E-A3)=3-1=2,
说明齐次方程组(0E-A1)x=0与(0E-A3)X=0都有两个线性无关的解，即对应于λ=0，矩
阵A1和A3都有2个线性无关的特征向量，所以矩阵A1和A3都与对角矩阵
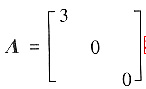相似，从而A1与A3相似.