问题
问答题
设f(x,y),φ(x,y)均有连续偏导数,点M0(x0,y0)是函数z=f(x,y)在条件φ(x,y)=0下的极
值点,又
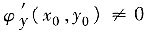 ,求证:
,求证:
(Ⅰ)
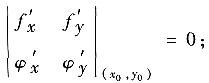
(Ⅱ)曲面z=f(x,y)与柱面f(x,y)=0的交线Γ在点P0(x0,y0,z0)(z0=f(x0,Y0))处的切
线与xy平面平行.
答案
参考答案:(Ⅰ)由题设条件
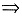 方程φ(x,y)=0在点M0邻域确定隐函数y=y(x),且满足y(x0)=y0.
方程φ(x,y)=0在点M0邻域确定隐函数y=y(x),且满足y(x0)=y0.
M0点是z=f(x,y)在条件φ(x,y)=0下的极值点
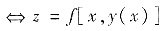 以x=x0为极值点,
以x=x0为极值点,
它的必要条件是
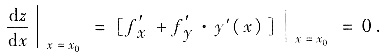 (*)
(*)
由φ[x,y(x)]=0及隐函数求导法得
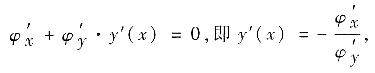
代入(*)得
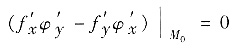 ,即
,即
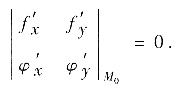
(Ⅱ)空间曲线
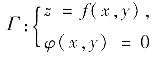 在P0(x0,y0,z0)处的切线的方向向量(切向量)为
在P0(x0,y0,z0)处的切线的方向向量(切向量)为
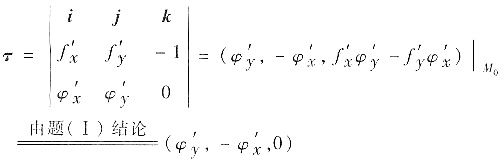
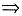 τ与xy平面平行.
τ与xy平面平行.
解析:本题的(Ⅱ)有如下变式:求证xy平面上的曲线f(x,y)=f(x0,y0)与曲线φ(x,y)=0在点M0处相切.
证明:曲线f(x,y)=f(x0,y0)与曲线φ(x,y)=0在公共点M0处的法向量分别是
 与
与
 ,由题(1)知,
,由题(1)知,
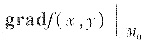 与
与
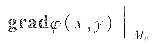 平行
平行
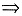 这两条曲线在点M0处相切.
这两条曲线在点M0处相切.
