问题
问答题
已知A是3阶矩阵，α1，α2，α3是3维线性无关列向量，且Aα1=3α1+3α2-2α3，Aα2=-α2，
Aα3=8α1+6α2-5α3.
(Ⅰ)写出与A相似的矩阵B；
(Ⅱ)求A的特征值和特征向量；
(Ⅲ)求秩r(A+E).
答案
参考答案：(Ⅰ)由于A(α1，α2，α3)=(3α1+3α2-2α3，-α2，8α1+6α2-5α3)
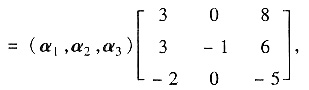
令P=(α1，α2，α3)，因α1，α2，α3线性无关，故P可逆.
记
则有P-1AP=B，即A与B相似.
(Ⅱ)由
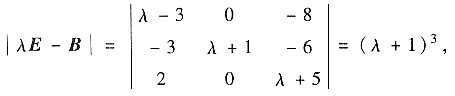
可知矩阵B的特征值为-1，-1，-1，故矩阵A的特征值为-1，-1，-1.
对于矩阵B，由
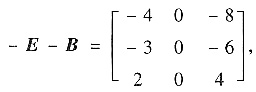得特征向量(0，1，0)T，(-2，0，1)T，
那么由Ba=λα即(P-1AP)α=λα，得A(Pα)=λ(Pα). 所以
是A的特征向量，于是A属于特征值-1的所有特征向量是
k1α2+k2(-2α1+α3)，其中k1，k2不全为0.
(Ⅲ)由A-B有A+E-B+E，故r(A+E)=r(B+E)=1.