问题
填空题
微分方程(2xsiny+3x2y)dx+(x3+x2cosy+y2)dy=0的通解是______.
答案
参考答案：
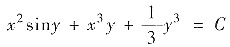，其中C为
常数.
解析：这不是一阶线性方程与变量可分离方程，也不是齐次方程与伯努利方程，因此，考察其是否是全微分方程. 将方程表为Pdx+Qdy=0，因在全平面上
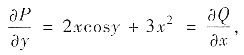
所以是全微分方程，求通解归结为求Pdx+Qdy的原函数u(x，y).
方法1°过凑微分法. 由于
(2xsiny+3x2y)dx+(x3+x2cosy+y2)dy
因此，通解为
其中C为
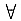常数.
方法2°不定积分法. 由
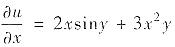，对x积分得
u=x2siny+x3y+C(y).
又由
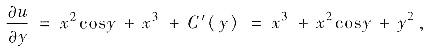
得
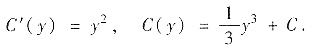
因此得通解
，其中C为
常数.
