问题
问答题
设矩阵A与B相似，其中
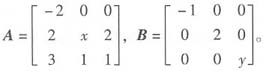
求x与y的值；
答案
参考答案：因为A～B，故其特征多项式相同，即|λE-A|=|λE-B|，
(λ+2)[λ2-(x+1)λ+(x-2)]=(λ+1)(λ-2)(λ-y)
令λ=0，得2(x-2)=2y，即y=x-2，
令λ=1，得y=-2，从而x=0。
搜题请搜索小程序“爱下问搜题”
设矩阵A与B相似，其中
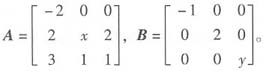
求x与y的值；
参考答案：因为A～B，故其特征多项式相同，即|λE-A|=|λE-B|，
(λ+2)[λ2-(x+1)λ+(x-2)]=(λ+1)(λ-2)(λ-y)
令λ=0，得2(x-2)=2y，即y=x-2，
令λ=1，得y=-2，从而x=0。