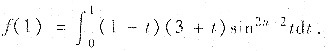问题
问答题
设n为自然数,
 证明:
证明:
(Ⅰ) f(x)在[0,+∞)取最大值并求出最大值点;
(Ⅱ)
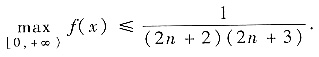
答案
参考答案:(Ⅰ)求f′(x),考察f(x)的单调性区间. 由于
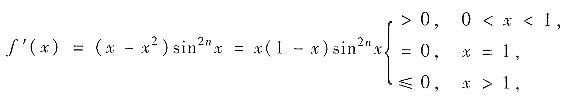
因此,当x>1时仅当x=kπ(k=1,2,…)时f′(x)=0. 于是,f(x)在[0,1]单调上升,f(x)
在[1,+∞)单调下降
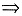
f(x)<f(1),x∈[0,+∞),x≠1.
因此,x=1是f(x)在[0,+∞)的唯一极值点且是极大值点,也是最大值点,从而
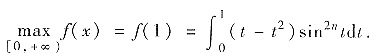
(Ⅱ)方法1°估计
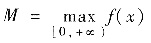 就是估计积分值
就是估计积分值
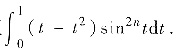 由sint≤t(t≥0)
由sint≤t(t≥0)
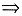
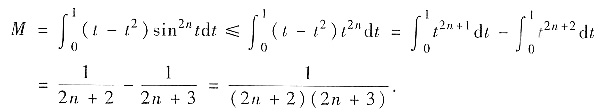
方法2°

因为当t≥1时,t-t2≤0,所以
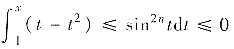 . 因此
. 因此
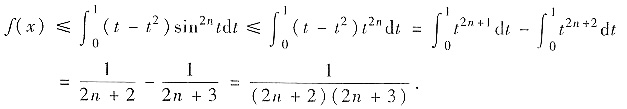
解析:本题有如下类似变式:已知函数y(x)满足(x+1)y″=y′,且y(0)=3,y′(0)=-2. 设n为自然数,
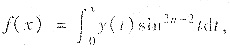 证明:
证明:
(Ⅰ)f(x)在[0,+∞)上取最大值并求出最大值点;
(Ⅱ)
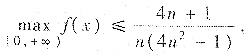
[提示]首先求满足所给方程及初始条件的解y(x)=(1-x)(3+x);然后按本题的方法求出最大值点x=1及最大值