问题
单项选择题
设流体的流速v=(x2+y2)j+(z-1)k，∑为锥面
，取下侧，则流体穿过曲面∑的体积流量是
A．
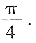
B．
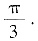
C．
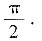
D．π.
答案
参考答案：B
解析：该流体穿过∑的体积流量是
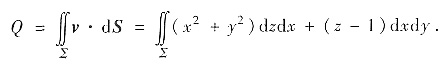
方法1°用高斯公式，∑不封闭，添加辅助面∑1：z=1(x2+y2≤1)，法向量朝上，∑与∑1围成区域Ω，取外侧.注意∑1与zOx平面垂直
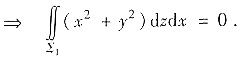
又在∑1上
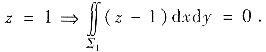在Ω上用高斯公式
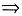
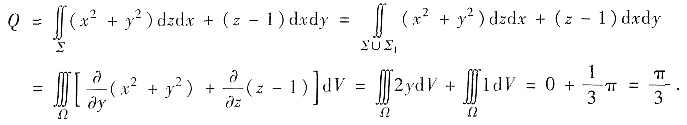这里，Ω关于zOx平面对称，2y对y为奇函数，
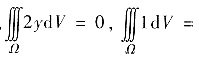圆锥体Ω的体积.故应选B.
方法2°直接计算，并对第二类面积分利用对称性，∑关于zOx平面对称，x2+y2对y为偶函数
又∑在xOy平面上的投影区域
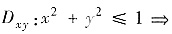
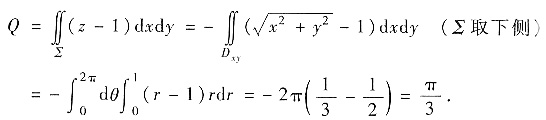
故应选B.
方法3°直接投影到xOy平面上代公式，
由∑的方程
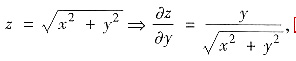又∑在xOy平面的投影区域Dxy：x2+y2≤1
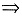
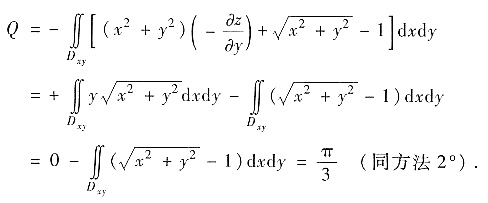
这里由于Dxy关于x轴对称，
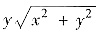对y为奇函数，所以
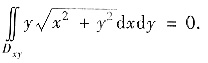故应选B.
