问题
填空题
设
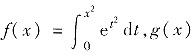在x=0连续且满足g(x)=1+2x +o(x)(x→0). 又F(x)=f[g(x)]，则F′(0)=______.
答案
参考答案：4e.
解析：由g(x)在点x=0处连续及g(x)=1+2x+o(x)(x→0)
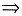
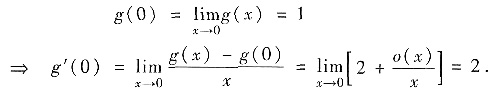
由复合函数求导法及变限积分求导法
搜题请搜索小程序“爱下问搜题”
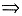
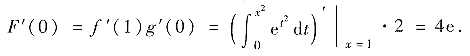
设
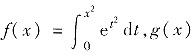在x=0连续且满足g(x)=1+2x +o(x)(x→0). 又F(x)=f[g(x)]，则F′(0)=______.
参考答案：4e.
解析：由g(x)在点x=0处连续及g(x)=1+2x+o(x)(x→0)
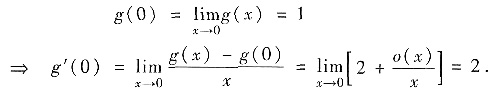
由复合函数求导法及变限积分求导法