问题
单项选择题
设A是m×n矩阵，则下列4个命题
①若r(A)=m，则非齐次线性方程组Ax=b必有解；
②若r(A)=m，则齐次方程组Ax=0只有零解；
③若r(A)=n，则非齐次线性方程组Ax=b有唯一解；
④若r(A)=n，则齐次方程组Ax=0只有零解
中正确的是
A．①③.
B．①④.
C．②③.
D．②④.
答案
参考答案：B
解析：因为A是m×n矩阵，若r(A)=m，说明A的行向量组线性无关，那么它的延伸组必线性无关. 所以必有
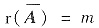. 从而
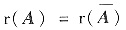，故线性方程组Ax=b必有解，①正确. 下面只需判断③或④正确即可.
若r(A)=n，说明A的列向量组线性无关，亦即Ax=0只有零解，所以④正确，故应选B.
当r(A)=m时，必有n≥m如果m=n，则Ax=0只有零解，而m＜n时，Ax=0必有非
零解，所以②不正确，
当r(A)=n时，
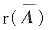有可能是n+1，方程组Ax=b可以无解，所以③不正确，你能举例说明吗？