问题
解答题
已知函数f(x)=
(Ⅰ)试作出函数f(x)图象的简图(请用铅笔作图,不必列表,不必写作图过程); (Ⅱ)请根据图象写出函数f(x)的定义域、值域、单调区间; (Ⅲ)若方程f(x)=a有解时写出a的取值范围,并求出当a=
|
答案
(1)∵f(x)=
,其图象如下:2x(x<0) (x-1)2(0≤x<2) 3-x(2≤x≤4)
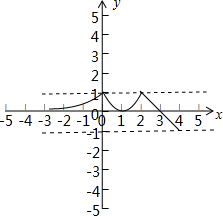
(2)由f(x)的图象可知,其定义域为:(-∞,4];值域:[-1,1];
单调递增区间:(-∞,0),(1,2),单调递减区间:(0,1),(2,4);
(3)由f(x)的图象可知,方程f(x)=a有解时a的取值范围[-1,1];
当a=
时,f(x)=1 2
.1 2
∴当x<0时,2x=
,解得x=-1;1 2
当0≤x<2时,(x-1)2=
,解得x=1±1 2
;2 2
当2≤x<4时,3-x=
,解得x=1 2
.5 2
