问题
问答题
设Q(x,y)在平面xOy上具有一阶连续的偏导数,且∫L2xydx+Q(x+y)dy与路径无关,且对任意的t有
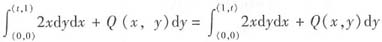 ,求Q(x,y)。
,求Q(x,y)。
答案
参考答案:因为曲线积分与路径无关,所以
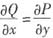 ,即
,即
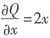 ,于是Q(x,y)=x2+φ(y)。
,于是Q(x,y)=x2+φ(y)。
由
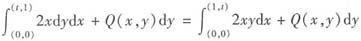 ,得
,得
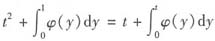 ,两边对t求导数得1+φ(t)=2t,φ(t)=2t-1,所以Q(x,y)=x2+2y-1。
,两边对t求导数得1+φ(t)=2t,φ(t)=2t-1,所以Q(x,y)=x2+2y-1。
解析:[考点] 利用曲线积分求原函数
设Q(x,y)在平面xOy上具有一阶连续的偏导数,且∫L2xydx+Q(x+y)dy与路径无关,且对任意的t有
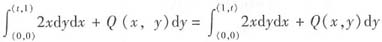 ,求Q(x,y)。
,求Q(x,y)。
参考答案:因为曲线积分与路径无关,所以
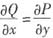 ,即
,即
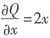 ,于是Q(x,y)=x2+φ(y)。
,于是Q(x,y)=x2+φ(y)。
由
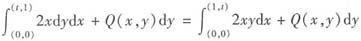 ,得
,得
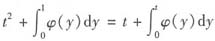 ,两边对t求导数得1+φ(t)=2t,φ(t)=2t-1,所以Q(x,y)=x2+2y-1。
,两边对t求导数得1+φ(t)=2t,φ(t)=2t-1,所以Q(x,y)=x2+2y-1。
解析:[考点] 利用曲线积分求原函数