问题
问答题
设函数f(x)在|x|≤1上有定义,在x=0的某个邻域内具有二阶连续导数,且
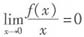 ,试证:级数
,试证:级数
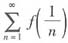 绝对收敛。
绝对收敛。
答案
参考答案:利用泰勒公式,首先由
 可知:
可知:
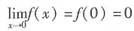 ,而且
,而且
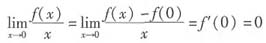
这样,利用函数f(x)的一阶泰勒公式,就有
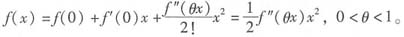
又因为f(x)在x=0的某一邻域内有连续的二阶导数,因此存在正数M,使|f"(x)|≤M在此邻域内成立,并且当n充分大时
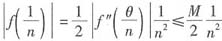 。
。
注意到级数
 绝对收敛,由比较判别法即知
绝对收敛,由比较判别法即知
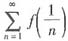 绝对收敛。
绝对收敛。
解析:[考点] 级数的收敛性
