问题
问答题
求函数f(x,y)=x2+4y2+9在D=(x,y)|x2+y2≤4上的最大值与最小值。
答案
参考答案:由题设,讨论f(x,y)=x2+4y2+9在约束条件x2+y2=4下的条件极值,
由拉格朗日乘数法,令F(x,y,λ)=x2+4y2+9+λ(x2+y2-4),
有
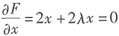 ,
,
 。
。
解得x=0,y=±2,λ=-4;x=±2,y=0,λ=-1。
f(0,2)=25,f(0,-2)=25,f(2,0)=13,f(-2,0)=13,f(0,0)=9。
所以f(x,y)在闭区域D上的最大值为25,最小值为9。
解析:[考点] 多元函数的板值
