阅读下列算法说明和流程图,根据回答下列问题。
[说明]
某机器上需要处理n个作业job1,job2,…,jobn,其中:
(1)每个作业jobi(1≤i≤n)的编号为i,jobi有一个收益值p[i]和最后期限值d[i];
(2)机器在一个时刻只能处理一个作业,而且每个作业需要一个单位时间进行处理,一旦作业开始就不可中断,每个作业的最后期限值为单位时间的正整数倍;
(3) job1~jobn的收益值呈非递增顺序排列,即p[1]≥p[2]≥...≥p[n];
(4)如果作业jobi在其期限之内完成,则获得收益p[i];如果在其期限之后完成,则没有收益。
为获得较高的收益,采用贪心策略求解在期限之内完成的作业序列。图8-22是基于贪心策略求解该问题的流程图。
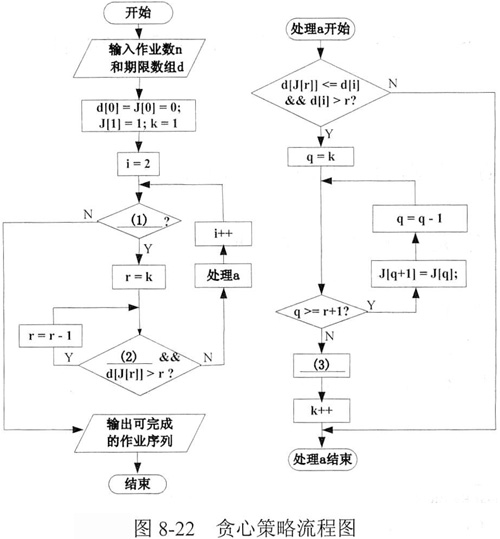
(1)整型数组J[]有n个存储单元,变量k表示在期限之内完成的作业数,J[1..k]存储所有能够在期限内完成的作业编号,数组J[1..k]里的作业按其最后期限非递减排序,即d[J[1]]≤...≤d[J[k]]。
(2)为了便于在数组J中加入作业,增加一个虚拟作业job0,并令d[0]=0,J[0]=0。
(3)算法大致思想是:先将作业job1的编号1放入J[1],然后,依次对每个作业jobi(2≤i≤n)进行判定,看其能否插入到数组J中。若能,则将其编号插入到数组J的适当位置,并保证J中作业按其最后期限非递减排列;否则不插入。
jobi能插入数组J的充要条件是:jobi和数组J中已有作业均能在其期限之内完成。
(4)流程图中的主要变量说明如下。
i:循环控制变量,表示作业的编号。
k:表示在期限内完成的作业数。
r:若jobi能插入数组J,则其在数组J中的位置为r+1。
q:循环控制变量,用于移动数组J中的元素。
[问题3]
对于本试题的作业处理问题,用图8-22的贪心算法能否求得最高收益______(能或不能)。用贪心算法求解任意给定问题时,是否一定能得到最优解______(能或不能)。
参考答案:能,或可以、行及其他含义相同的词语
不能,或不可以、不行及其他含义相同的词语
解析:这是一道判断贪心算法是否能求得最优解的应用分析题。对于本试题的作业处理问题,用图8-22的贪心算法策略,能求得最优解(即能求得最高收益)。但不是所有的问题都能通过贪心策略来求得最优解,一个典型的例子是0-1背包问题。例如,有3件物品,背包可容纳50磅重的东西,每件物品的详细信息如表8-10所示,问如何装包使得其价值最大
| 物品编号 | 重量(磅) | 价值(美元) | 单位价值 |
| R | 10 | 60 | 6 |
| S | 20 | 100 | 5 |
| T | 30 | 120 | 4 |
