问题
问答题
阅读以下说明,根据要求回答问题。
[说明]
系统集成商QD公司最近承接了一个中小型系统集成项目工程。该工程项目经理小谢经过工作分解后,已经明确此项目的范围,但是为了更好地对项目的实施过程进行有效监控,保证项目按期、保质地完成,小谢需要采用网络计划技术对项目进度进行管理。该集成项目包括A~H共8个基本活动。这些活动的名称、完成每个活动所需的时间,以及其他活动之间的关系如表所示。
| 表 某系统集成项目活动基本情况 | |||||
| 活动名称 | 所需的时间(天) | 紧前活动 | 法动名称 | 所需的时间(天) | 前置活动 |
| A | 5 | —— | E | 8 | B |
| B | 10 | A | F | 20 | D,E |
| C | 20 | A | G | 22 | C,D |
| D | 15 | B,C | H | 10 | F,G |
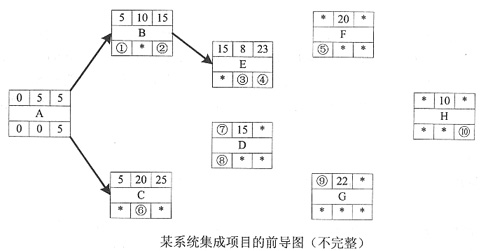
图1
图1中各节点使用如图2所示的样图标识。

图2
图例说明:
ES:最早开始时间 EF:最早结束时间 DU:作业历时 ID:作业代号
LS:最迟开始时间 LF:最迟完成时间 TF:总浮动时间
为了加快项目进度,在进行活动D、G时项目经理采取了适当加班(赶工)的措施,因此将活动D的时间压缩了5天(历时10天)、活动G的时间压缩了2天(历时20天)。请指出此时项目的关键路径,并计算项目工期,以及活动E的总浮动时间、最晚开始时间。
答案
参考答案:项目的关键路径有两条,即路径ACDFH和路径ACDGH
项目工期为65天
活动E的总浮动时间为12天
活动E的最晚开始时间为第27天
解析:为了加快项目进度,在进行活动D、G时项目经理采取了适当加班(赶工)的措施,因此将活动D的时间压缩了5天(即由原来的历时15天变为历时10天),活动G的时间压缩了2天(即由原来的历时22天变为历时20天)。此时,需要重新计算图3各条路径的时间跨度,如表所示。
| 表 某项目各条路径的工期(变更后) | |||||
| 序号 | 路径 | 工期(天) | 序号 | 路径 | 工期(天) |
| 1 | ABEFH | 5+10+8+20+10=53 | 4 | ACDFH | 5+20+10+20+10=65 |
| 2 | ABDFH | 5+10+10+20+10=55 | 5 | ACDGH | 5+20+10+20+10=65 |
| 3 | ABDGH | 5+10+10+20+10=55 | 6 | ACGH | 5+20+20+10=55 |
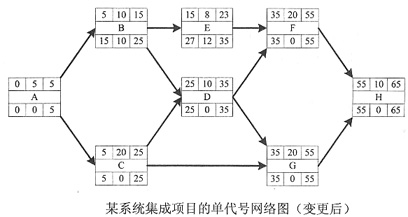
图4
活动E的最晚结束时间(LFE)取决于活动F的最晚开始时间(LSF),即第35天;而活动E的最早结束时间(EFE)仍为第23天;因此活动E的总浮动时间(TFE)=LFE-EFE=35-23=12天。活动E的最晚开始时间(LSF)=LFF-DUF=35-8=27,即第27天。
