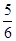（1）100；（2）①；②．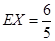

题目分析：

解题思路：（1）根据分层抽样的特点“等比例抽样”求解即可；（2）①利用古典概型概率公式以及对立事件概率公式求解；②利用超几何分布的概率公式求概率，再求期望即可.

规律总结：1.遇到“至少”、“至多”，且正面情况较多时，可以考虑对立事件的概率；2.利用概率或随机变量的分布列以及期望、方差解决应用题时，要注意随机变量的实际意义.

试题解析：（1）由题意，得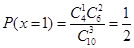

∴n=100                                        

（2）设所选取的人中有m人在40岁以下

则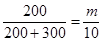，解得m=4                          

①记“至少一人在40岁以下”为事件A

则                                   

②X的可能取值为0,1,2,3

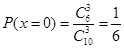
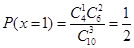
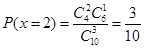
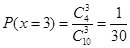
∴x的分布列为

X	0	1	2	3
P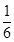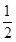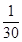

.
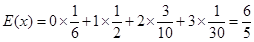