问题
问答题
(1)证明:利用变换
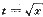 可将方程
可将方程
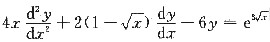 化为
化为
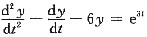 ;
;
(2)求原方程的通解.
答案
参考答案:[详解] (1)[*],则x=t2,dx=2tdt,于是
[*]
代入原方程中,得
[*]
整理得
[*]
(2)特征方程为λ2-λ-6=0,解得λ1=3,λ2=-2,齐次方程的通解为
[*]
再求原方程的特解,设y*=Ate3t,
则 y*’=Ae3t+3Ate3t, y*"=6Ae3t+9Ate3t
代入原方程可求得[*]所求特解为[*]
故原方程的通解为
[*]
解析:
[分析]: 本题是作自变量变换,关键注意求导公式:[*],至于第二步求通解则是基础问题.
[评注] 除了作自变量变换t=h(x)外,本题还可从要求作函数变换u=ψ(y),以及同时作函数变换u=ψ(y)与自变量交换t=h(x)等角度进行考查.
