问题
问答题
设函数
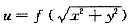 ,满足
,满足
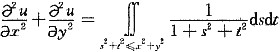 ,且
,且
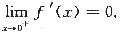
(1)试求函数f’(x)的表达式;
(2)若f(0)=0,求

答案
参考答案:[详解] (1)设[*],则
[*]
同理,[*]
而 [*]
于是 [*]
解此微分方程,得
[*]
即 [*]
又 [*]
知 [*] 故[*]
(2)利用洛必达法则.有
[*]
解析:
[分析]: 先求出二阶偏导数与二重积分,代入已知等式后可得一关于f(r)的二阶微分方程.注意此微分方程是可降阶的(或当作一阶线性微分方程),由此可解得f’(r)的表达式,并且根据极限条件确定相应的常数.至于极限问题,首先利用洛必达法则,再代入f’(r)的表达式即可求出极限.
[评注] 本题综合考查了极限、偏导、二重积分和微分方程等多个知识点,但每一步的求解均是基本要求.
