问题
填空题
设曲线y=f(x)在原点处与y=sinx相切,a,b为常数,ab≠0,则
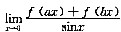 =______.
=______.
答案
参考答案:a+b
解析:
[分析]: 已知曲线y=f(x)在原点处与y=sinx相切,相当于已知f(x)在点x=0处的函数值f(0)与导数值f’(0),再根据导数的定义即可得要求的极限.
[详解] 由题设知,f(0)=sin0=0,f’(0)=(sinx)’|x=0=cos0=1,于是
[*]
[评注] 本题条件f(0)=0很重要,否则待求函数极限的分子部分极限非零,整个极限不存在,或要求将分子改为“f(ax)~f(bx)”,才能求极限.
