(本小题满分13分)
定义F(x,y)=(1+x)y,其中x,y∈(0,+∞).
(1)令函数f(x)=F(1,log2(x3+ax2+bx+1)),其图象为曲线C,若存在实数b使得曲线C在x0(-4<x0<-1)处有斜率为-8的切线,求实数a的取值范围;
(2)令函数g(x)=F(1,log2[(lnx-1)ex+x]),是否存在实数x0∈[1,e],使曲线y=g(x)在点x=x0处的切线与y轴垂直?若存在,求出x0的值;若不存在,请说明理由.
(3)当x,y∈N,且x<y时,求证:F(x,y)>F(y,x).
(1)a<10.
(2)略
(3)略
解:(1)f(x)=F(1,log2(x3+ax2+bx+1))=x3+ax2+bx+1,设曲线C在x0(-4<x0<-1)处有斜率为-8的切线,
又由题设知log2(x3+ax2+bx+1)>0,f′(x)=3x2+2ax+b,
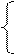 3x20+2ax0+b="-8 " ①
3x20+2ax0+b="-8 " ①
∴存在实数b使得 -4<x0<-1 ② 有解,(3分)
x30+ax20+bx0>0 ③
由①得b=-8-3x-2ax0,代入③得-2x-ax0-8<0,
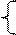 ∴由 2x20+ax0+8>0 有解,
∴由 2x20+ax0+8>0 有解,
-4< x0<-1
得2×(-4)2+a×(-4)+8>0或2×(-1)2+a×(-1)+8>0,
∴a<10或a<10,∴a<10.(5分)
(2)∵g(x)=(lnx-1)ex+x,
∴g′(x)=(lnx-1)′ex+(lnx-1)(ex)′+1=+(lnx-1)ex+1=(+lnx-1)ex+1.(6分)
设h(x)=+lnx-1.则h′(x)=-+=,
当x∈[1,e]时,h′(x)≥0.
h(x)为增函数,因此h(x)在区间[1,e]上的最小值为ln1=0,即+lnx-1≥0.
当x0∈[1,e]时,ex0>0,+lnx0-1≥0,
∴g′(x0)=(+lnx0-1)ex0+1≥1>0.(8分)
曲线y=g(x)在点x=x0处的切线与y轴垂直等价于方程g′(x0)=0有实数解.
而g′(x0)>0,即方程g′(x0)=0无实数解.
故不存在实数x0∈[1,e],使曲线y=g(x)在点x=x0处的切线与y轴垂直.(9分)
