目前的股票价格为45元，执行价格为52元，距离到期的时间为6个月，股价的方差为 0.04，无风险年利率为0.065。 (1)根据上述特征利用布莱克一斯科尔斯期权定价模型计算看涨期权的价值。 (2)依据买卖权平价计算对应的看跌期权的价值。
参考答案：
解析：(1)计算看涨期权的价值：
①
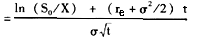
=[+(0.065+×0.04)×0.5]/(0.2×
)
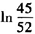=(-0.1446+0.0425)/0.1414
=-0.7221
②d2=d1-
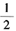
=-0.7221-0.2×
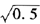
=-0.8635
③通过N(0.72)=0.7642和N(0.73)=0.7673之间插值来计算N(0.7221)：
N(0.7221)=0.7642+
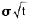×(0.7673-0.7624)=0.7649
N(-0.7221)=1-N(0.7221)=1-0.7649=0.2351
通过N(0.86)=0.8051和N(0.87)=0.8078之间插值来计算N(0.8635)：
N(0.8635)=0.8051+
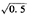×(0.8078-0.8051)=0.8060
N(-0.8635)=1-N(0.8635)=1-0.8060=0.194
C0=S0N(d1)-Xe-retN(d2)
=45×0.2351-52×e-0.065×0.5×0.194
=10.58-9.77
=0.81(元)
(2)计算看跌期权的价值：
依据买卖权平价：标的资产现行价格+看跌期权价格-看涨期权价格=执行价格的现值
则：看跌期权价值=看涨期权价格+执行价格的现值-标的资产现行价格
=0.81+52×e0.065×0.5-45=0.81+50.34-45=6.15 (元)
或者为了简化起见，执行价格的现值=52/(1+0.065/2)=50.36(元)，则看跌期权价值=看涨期权价格+执行价格的现值-标的资产现行价格=0.81+50.36-45=6.17 (元)。