问题
问答题
已知
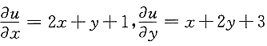，u(0，0)=1，求u(x，y)及其极值．
答案
参考答案：
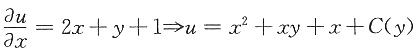，两边对y求导得
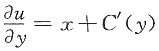与
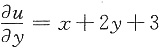对比后得
C’(y)=2y+3，两边积分得
C(y)=y2+3y+C，
于是有
，
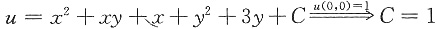因此有u=x2+xy+x+y2+3y+1．
令
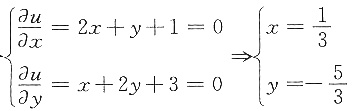
又
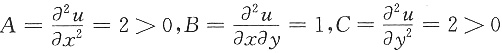
B2-AC=-3＜0，
所以u(x，y)在
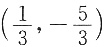处取得极大值
．
搜题请搜索小程序“爱下问搜题”
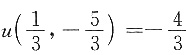已知
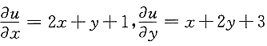，u(0，0)=1，求u(x，y)及其极值．
参考答案：
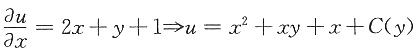，两边对y求导得
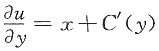与
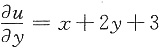对比后得
C’(y)=2y+3，两边积分得
C(y)=y2+3y+C，
于是有
，
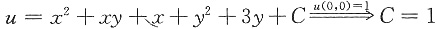因此有u=x2+xy+x+y2+3y+1．
令
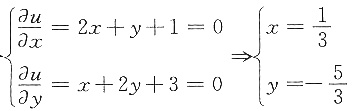
又
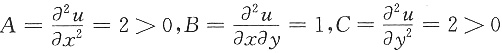
B2-AC=-3＜0，
所以u(x，y)在
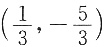处取得极大值
．
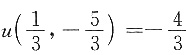