参考答案：B

解析：[详解] 由于向量组α₁，α₂，…，α_s是齐次线性方程组Ax=0的一个基础解系，则α₁，α₂，…，α_s线性无关，且满足Aα_i=0(i=1，2，…s)；
向量β不是方程组Ax=0的解，则Aβ≠0．
设存在一组常数k，k₁，k₂，…，k_s，使得
kβ+k₁(β+α₁)+k₂(β+α₂)+…+k_s(β+α_s)=0， ①
上式两边左乘A，则有
kAβ+k₁A(β+α₁)+k₂A(β+α₂)+…+k_sA(β+α_s)=0，
(k+k₁+…+k_s)Aβ+k₁Aa₁+k₂Aα₂+…+k_sAα_s=0，
(k+k₁+…+k_s)Aβ=0

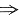k+k₁+…+k_s=0，
将k+k₁+…+k_s=0代入①式可得k₁α₁+k₂α₂+…+k_sα_s=0，
因为α₁，α₂，…，α_s线性无关，所以k₁=k₂=…k_s=0，k=-k₁-…-k_s=0，
故β，β+α₁，β+α₂，…，β+α_s线性无关．