问题
单项选择题
在圆x2+y2-6x-8y+21=0所围区域(含边界)中，P(x，y)和Q(x，y)是使得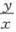
分别取得最大值和最小值的点，线段PQ的长是（）。
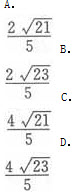
A.A
B.B
C.C
D.D
答案
参考答案：C
解析：
圆的方程可化为：(x-3)2+(y-4)2=22，即圆心为O’(3，4)，半径为2，整个圆处于第一象限。直线y=kx与圆相切时，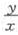
取得最大值和最小值，如图所示，上下切点即为P和Q。连接O’P，O’Q，PQ和OO’。根据圆的切线的性质，O’P=O’Q=2，∠OPO’=∠OQO’=90°，则△OPO’≌△OQO’，OO’平分∠PO’Q，OO’⊥PQ且平分PQ于点M。长度OO’=
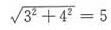。则在Rt△OO’Q中，
，
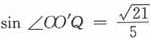。在Rt△O’MQ中，
=
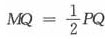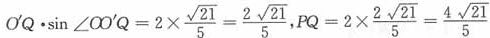，故应选C。
