问题
单项选择题
f(x)，g(x)是连续函数，且
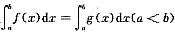，则必有( )。
(A) 曲线y=f(x)与y=g(x)在[a，b]上重合
(B) 曲线y=f(x)与y=g(x)仅在x=a与x=b相交
(C) 曲线y=f(x)与y=g(x)在[a，b]上至少有一个交点
(D) 不能确定曲线y=f(x)与y=g(x)在[a，b]上是否有交点
答案
参考答案：C
解析： 设
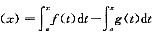，则F(a)=F(b)=0，F(x)在[a，b]上连续，在(a，b)内可导，由罗尔定理，至少存在ξ∈(a，b)使得F’(ξ)=0，而F’(x)=f(x)-g(x)，F’(ξ)=0，即F(ξ)-g(ξ)=0。
故选(C)
评注也可用积分中值定理解析本题，因
，所以
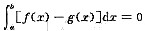
从而存在ξ∈[a，b]使得[f(ξ)-g(ξ)](b-a)=0，即有f(ξ)-g(ξ)=0