问题
单项选择题
如果函数y=sin2x+acos2x的图像关于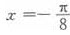
对称，那么a=（）。
A．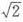
B．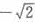
C．1
D．-1
答案
参考答案：D
解析：
解法1：因为
，
根据正弦函数的图像知：在对称轴处y达到最值，
故
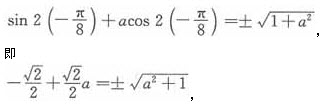
故(a+1)2=0，
得a=-1，故正确答案为D。
解法2：y=f(x)=sin2x+acosx的图像关于
对称，所以
(其中x∈R)，
故
，
利用和差化积公式化简，得
(a+1)·sin2x=0(x∈R)，
故a+1=0，即a=-1，
故正确答案为D。