问题
单项选择题
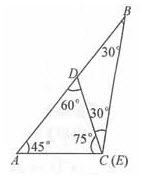
△ABC中，∠A:∠B:∠C=3:2:7，如果从AB上的一点D做射线l，交AC或BC边于点E，使∠ADE=60°，且l分△ABC所成两部分图形的面积相等，那么（）。
A．l过C点(即E点与C重合)
B．l不过C点而与AC相交
C．l不过C点而与BC相交
D．l不存在
答案
参考答案：B
解析：
如图，因在△ABC中，∠A:∠B:∠C=3:2:7且∠A+∠B+∠C=180°，故有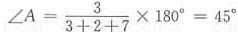
，
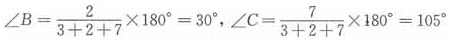。考虑临界位置，即C与E重合，此时由于∠ADE=60°，则∠ACD=75°，∠DCB=30°，且得到DC=DB。在△ACD中，因为75°＞45°，所以AD＞DC=DB。
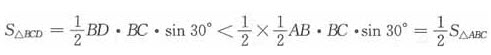。又因∠ADE=60°恒成立，欲使DE分△ABC为面积相等的两块，DE应向左方平移，即射线l不过C点而与AC相交，故应选B。
