问题
问答题
设f(x)为连续函数，
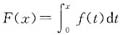．试证明：
1.F(x)的奇偶性正好与f(x)的奇偶性相反．
答案
参考答案：设f(x)具有周期T，记
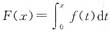，考察
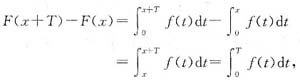
所以F(x)以T为周期的充要条件是
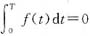．而f(x)的任意一个原函数可以表示成F(x)+C，当且仅当F(x)为T周期时，F(x)+C以T为周期，所以f(x)的任意一个原函数以T为周期的充要条件是
搜题请搜索小程序“爱下问搜题”
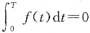
设f(x)为连续函数，
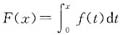．试证明：
1.F(x)的奇偶性正好与f(x)的奇偶性相反．
参考答案：设f(x)具有周期T，记
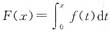，考察
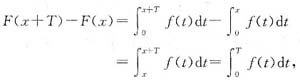
所以F(x)以T为周期的充要条件是
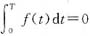．而f(x)的任意一个原函数可以表示成F(x)+C，当且仅当F(x)为T周期时，F(x)+C以T为周期，所以f(x)的任意一个原函数以T为周期的充要条件是