问题
填空题
已知函数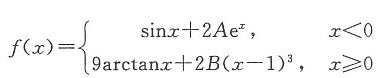
在x=0有一阶导数,则A=(),B=()。
答案
参考答案:A=1,B=-1
解析:
利用函数在一点连续的定义及函数在一点可导的必要条件,可建立A与B的两个方程.联立解之,即可求得A与B的值.立A与B的两个方程.联立解之,即可求得A与B的值.
因连续是可导的必要条件,所以
f(0-0)=f(0+0)=f(0),
而
f(0-0)=2A, f(0+0)=-2B, f(0)=-2B,
故A=-B.又由
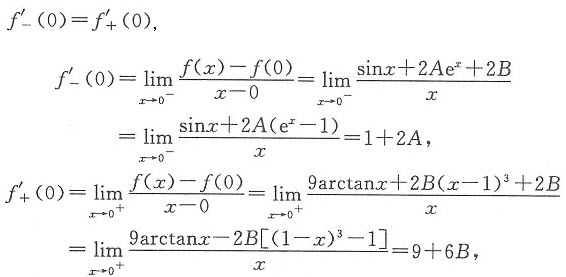
可得1+2A=9+6B.又因A=-B,故9-6A=1+2A,于是A=1,B=-1.
