给定矩阵
其行向量都是齐次线性方程组(Ⅰ):
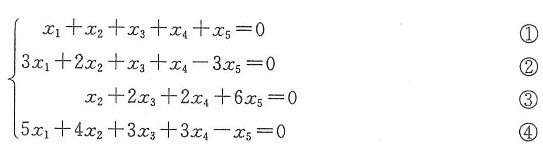
的解向量.问:B的4个行向量是否构成方程组(Ⅰ)的基础解系若不能,不用解方程组的方法.试求方程组(Ⅰ)的一个基础解系。
参考答案:
先用观察法找出方程组(Ⅰ)所包含的独立方程的个数.这样易求出其系数矩阵A的秩(当然,也可用初等行变换求之).事实上,有
2×①+②=④,
3×①-②=③.
因而方程组(Ⅰ)中的方程①与②是独立方程组,其系数矩阵A的秩为2.又n=5,故方程组(Ⅰ)的一个基础解系只含5-2=3个解向量.因而只需找出B中3个线性无关的行向量即可.
令B中的第1,2,4个行向量分别为
β1=[1,-2,1,0,0]T,β2=[1,-2,0,1,0]T,β4=[5,-6,0,0,1]T.
因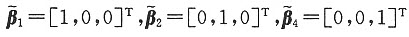 ,显然线性无关,在其相同位置上增加相同个数的分量(2个分量),即得到β1,β2,β4.它们仍然线性无关,于是它们可作为方程组(Ⅰ)的一个基础解系.
,显然线性无关,在其相同位置上增加相同个数的分量(2个分量),即得到β1,β2,β4.它们仍然线性无关,于是它们可作为方程组(Ⅰ)的一个基础解系.
而B中第3个行向量
β3=[1,-2,3,-2,0]T=3β1-2β2+0β4
即为β1,β2,β4的线性组合.故B中4个行向量不能组成方程组(Ⅰ)的基础解系.
事实上,方程组(Ⅰ)的一个基础解系只含3个解向量.当然这3个解向量不唯一.事实上,β1,β3,β4也是方程组(Ⅰ)的一个基础解系.