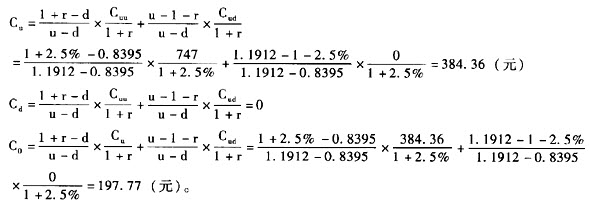假设某公司股票目前的市场价格为25元，而在6个月后的价格可能是32元和18元两种情况。再假定存在一份100股该种股票的看涨期权，期限是半年，执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金，同时售出一份100股该股票的看涨期权。
要求：
(1)根据单期二叉树期权定价模型，计算一份该股票的看涨期权的价值。
(2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变，若把6个月的时间分为两期，每期3个月，若该股票收益率的标准差为0.35，计算每期股价上升百分比和股价下降百分比。
(3)结合(2)分别根据套期保值原理、风险中性原理和两期二叉树期权定价模型，计算一份该股票的看涨期权的价值。
参考答案：
(1)股价上升百分比=(32-25)/25=28%
股价下降百分比=(18-25)/25=-28%
期权的价值C0=[W1×Cu+(1-W1)×Cd]÷(1+r)
将r=5%，u=1.28，d=1-0.28=0.72，Cu=400，Cd=0代入上式。
期权的价值
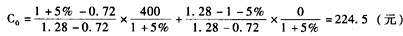
(2)u=1+上升百分比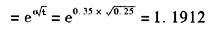
，上升百分比=19.12%
d=1-下降百分比=1/u=1/1.1912=0.8395，下降百分比=16.05%
(3)①根据套期保值原理：
套期保值比率
借入资金数额
Cu=购买股票支出-借款=H2Su-Y2=71.35×29.78-1740.24=384.56(元)
Cd=0
套期保值比率
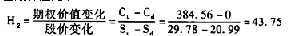
借入资金数额
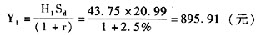
C0=购买股票支出-借款=H1S0-Y1=43.75×25-895.91=197.84(元)
②根据风险中性原理：
期望报酬率=上行概率×股价上升百分比+下行概率×股价下降百分比
=上行概率×股价上升百分比+(1-上行概率)×股价下降百分比
即：2.5%=上行概率×19.12%+(1-上行概率)×(-16.05%)
上行概率=52.74%
期权价值6个月后的期望值=52.74%×747+(1-52.74%)×0=393.97(元)
Cu=393.97/(1+2.5%)=384.36(元)
期权价值3个月后的期望值=52.74%×384.36+(1-52.74%)×0=202.71(元)
期权的现值=202.71/(1+2.5%)=197.77(元)
③根据两期二叉树期权定价模型：
