问题
单项选择题
若正数a，b满足ab=a+b+3，则ab的取值范围是（）。
A．(1，3)
B．[9，+∞)
C．[1，5]
D．(1，9]
答案
参考答案：B
解析：
由ab=a+b+3，得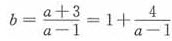
，两边同乘以a，得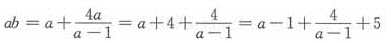
又由ab=a+b+3，得b(a-1)=a+3＞0，故a-1＞0，故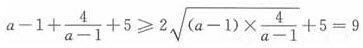
。
所以当目仅当a=3时取等号，因而取信范围是[9，+∞)，故正确答案为B。
搜题请搜索小程序“爱下问搜题”
若正数a，b满足ab=a+b+3，则ab的取值范围是（）。
A．(1，3)
B．[9，+∞)
C．[1，5]
D．(1，9]
参考答案：B
解析：
由ab=a+b+3，得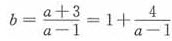，两边同乘以a，得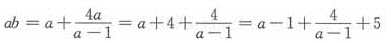
又由ab=a+b+3，得b(a-1)=a+3＞0，故a-1＞0，故。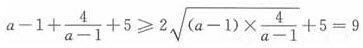
所以当目仅当a=3时取等号，因而取信范围是[9，+∞)，故正确答案为B。