问题
填空题
设三次多项式f(x)=ax3+bx2+cx+d满足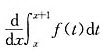
=12x2+18x+1，则f(x)的极大值点为=（）。
答案
参考答案：-1．
解析：
由题设的等式，有
f(x+1)-f(x)=12x2+18x+1，即有3ax2+(3a+2b)x+(a+b+c)=12x2+18x+1．
解方程组
可得a=4，b=3，c=-6，即有f(x)=4x2+3x2-6x+d，从而可知
f’(x)=12x2+6x-6， f’’(x)=24x+6，所以f(x)有极值点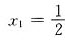
，x2=-1，由
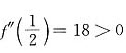，f’’(-1)=-18＜0，可知函数f(x)的极大值点应为x=-1．